中值定理:考证明题,10'(①4‘+②6’)
十大定理(1-4为f(x),5-9为f'(x),10为)
- 定理1—有界与最值定理
- 定理2—介值定理
- 定理3—平均值定理
- 定理4—零点定理
- 定理5—费马定理
- 定理6—罗尔定理
- 定理7—拉格朗日中值定理
- 定理8—柯西中值定理
- 定理9—泰勒公式
- 定理10—积分中值定理
一、涉及函数的中值定理
1、定理1(有界与最值定理)
2、定理2(介值定理)
3、定理3(平均值定理/离散的的平均值定理)
注:
定理3是(离散的)平均值定理:
定理10是(连续的)平均值定理:
4、定理4(零点定理)
当时,存在()使得(端点异号,经过轴,由介值定理推论)
例题
1、设在上连续,当时,证明存在使得.
分析:由最值定理,所以,,,所以
2、设在上连续,当时,证明存在使得.
二、设计导数(微分)的中值定理
5、定理5(费马定理)
设满足在点处①可导②取极值则
费马大定理:,没有正整数解。
证明:
证明导数在某一点等于几,用定义。

6、定理6(罗尔定理)
设满足①在上连续②在内可导,则存在()使得③
7、定理7(拉格朗日中值定理)
$设f(x)满足\left{
\begin{aligned}
① && 在[a,b]上连续, \
② && 在(a,b)内可导 \
\end{aligned}
\right. $
则存在()使得
或者写成
8、定理8(柯西中值定理)
设满足①在上连续②在内可导,则存在()③
使得
9、定理9(泰勒公式)
10、定理10(积分中值定理/连续的平均值定理)
设在上连续,证明存在使得
证明:
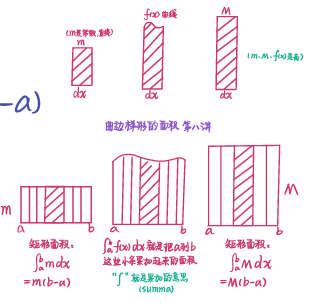
①最值原理由于在上连续,则有最大值和最小值⇩⇩⇩⇩⇩②介值定理⇩⇩存在,使⇩⇨⇨


